Ironicwarcriminal posted:Shanghai Metro
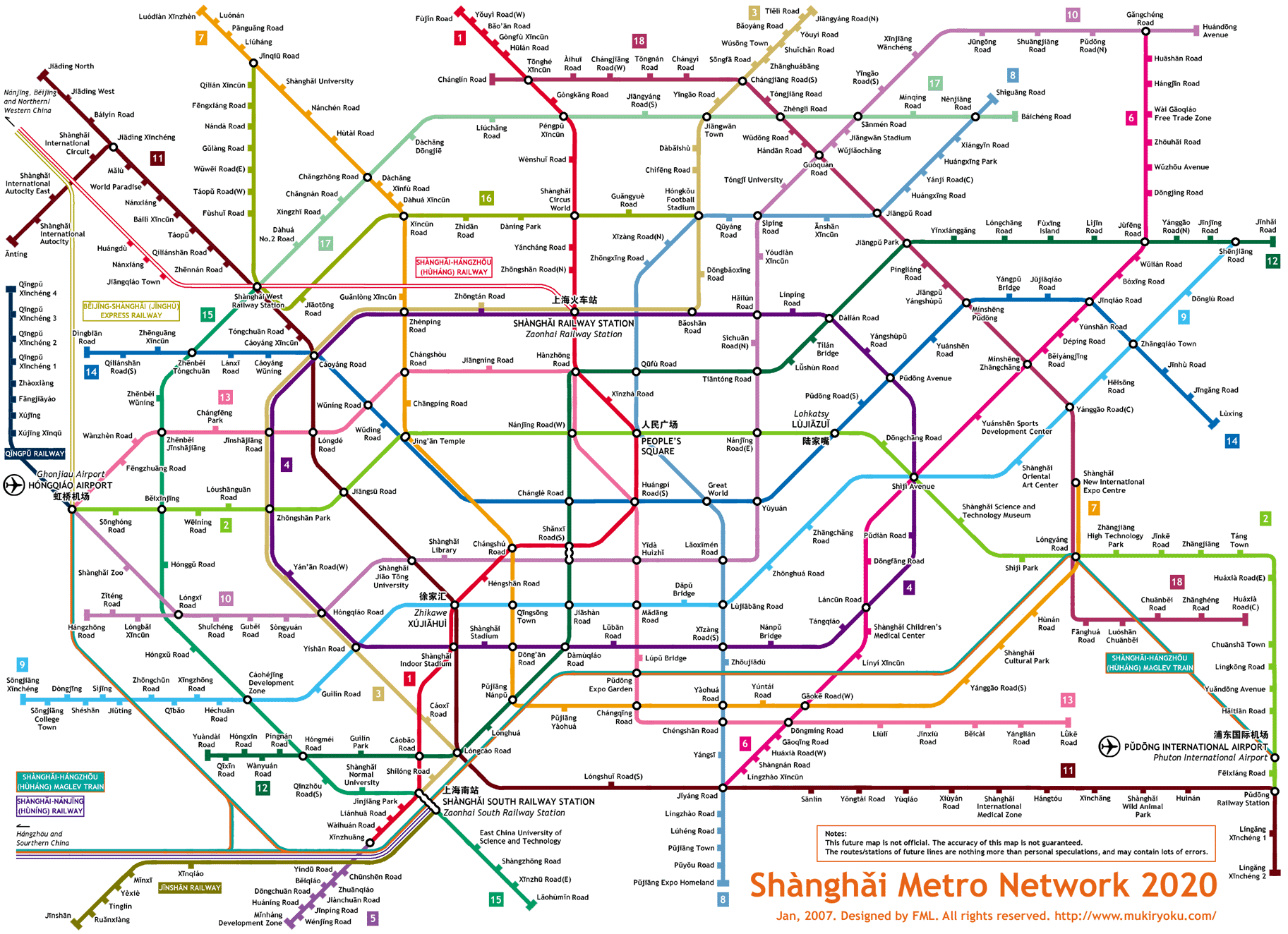
the first line opened in 1995, pretty stunning
Designed by FML
Ironicwarcriminal posted:The London-Paris train was pretty cool. You just enter a tunnel in Kent and 15 minutes later you come out of a tunnel and there are renaults and Peugeots and better houses and nicer villages and sunshine
lol are you kidding the area round calais is horrible
discipline posted:the metro in dc looks like something out of fascist space AND the future.

deadken posted:Ironicwarcriminal posted:
The London-Paris train was pretty cool. You just enter a tunnel in Kent and 15 minutes later you come out of a tunnel and there are renaults and Peugeots and better houses and nicer villages and sunshine
lol are you kidding the area round calais is horrible
i thought it was rustic and quaint
the irritating thing is that although there are a festering dizzy of new transit plans for within Toronto's sorely underserved daughter cities afaik no-one seems to be thinking of improving transport links between the metropolis and the outskirts. i mean the only way to get to missisauga from downtown is to drive or take the bus from Islington which has to putter along deeply congested roads. there's the University shuttle as well, which takes the highway and is even worse. my wife is starting a new job out there on Friday and will probably have to get out of the house at 7.15 for a 9am start. missisauga is approximately 25km away btw.
Edited by littlegreenpills ()
littlegreenpills posted:i just took a mouthful of coffee and there was a roach in it.
:S

I've always been partial to grainers, just because you can fit in that little hole in the back. It's like a little crusty den. If I were to ride trains, I'd def ride grainers.

Lol look at that crusty

I've always been partial to grainers, just because you can fit in that little hole in the back. It's like a little crusty den. If I were to ride trains, I'd def ride grainers.

Lol look at that crusty
innsmouthful posted:bunch of friggin public transit yuppies itt. thread needs more freight.
ive been resisting urge to post about NYC subway but tonight ill probably post about it. Owne
swampman posted:ive been resisting urge to post about NYC subway but tonight ill probably post about it. Owne
if you do that i will be forced to retaliate in ways you cannot possibly begin to imagine
swampman posted:
I never used to pay as a teen either. I've been riding the Max off and on for 10 years now, and it's only this year I saw my first fare inspector.
it introduces people to winter sports AND the wonders of rail travel
Ironicwarcriminal posted:discipline posted:stop being jelly coz you never been on a train in that hellhole peninsula you call florida
Hey yo I was reading some stuff on Jax on a planning website just yesterday and in a new area the developer/city was being “socially responsible” by installing wheelchair pads at bus stops.
They refuse to build any sidewalks though, too funny.
jacksonville rules. they built a highway for the sole purpose of cordoning off downtown from de blecks and called it the martin luther king jr parkway
littlegreenpills posted:sorry dude ive seen the light now. trains are for bulk materials only. if you don't go everywhere by moped or giving blowjobs to truckers you are insufficiently aesthetic and must be purged
*skateboards

